Page 36 - Revista Aranduka_Vol10 Nº 01 Web

36 INVESTIGACIÓN INVESTIGACIÓN 37

Índice de criticidad de rutas IV. CONCLUSIÓN

Distribución Ruta A Ruta B
Uniforme 0,9677 0,0323 Tras haber aplicado el modelo PERT, y el método minar el proyecto en un tiempo mucho mayor a su
de simulación de Montecarlo, para hallar la dura- media, es menor que en las demás distribuciones;
PERT modificada (λ=1) 0,9799 0,0201 ción media del proyecto, se ha observado cierta ya que los valores alrededor de la media se encuen-
PERT modificada (λ=2) 0,9877 0,0123 discrepancia entre los resultados obtenidos. Cabe tran más dispersos que en las demás distribuciones
PERT modificada (λ=3) 0,9925 0,0075 resaltar que las diferencias entre la duración media generadas. En consecuencia, la distribución de pro-
arrojada por el modelo PERT y, cada una de las babilidad frecuencial de la duración del proyecto,
Triangular 0,9932 0,0068
duraciones medias arrojada por las nueve corridas hallada a partir de la distribución uniforme, es la
PERT (λ=4) 0,9956 0,0044 simultáneas de simulación, ha sido menor a 8 días más pesimista de todas las halladas. Sin embargo,
PERT modificada (λ=5) 0,9974 0,0026 en todos los casos. En consecuencia, la mencionada cabe resaltar que, por simple inspección visual todas
PERT modificada (λ=6) 0,9986 0,0014 diferencia es menor a 2,20% de la duración media las gráficas de la Figura 3 tienen una forma similar
PERT modificada (λ=7) 0,9989 0,0011 arrojada por el modelo PERT. La mayor de dichas a la de la distribución normal.
diferencias es la existente entre la media dada
por PERT (363,8333 días corridos) y, la media de la Tras haber efectuado las nueve corridas simultá-
Tabla 2. Índice de criticidad de las rutas. distribución generada a partir de la aplicación de neas, solo dos rutas de las veinticinco existentes
la distribución uniforme (371,6130 días corridos); han resultado ser críticas; éstas son las rutas A y B.
además, la varianza de la primera corresponde a Es importante aclarar que en ninguna iteración, la
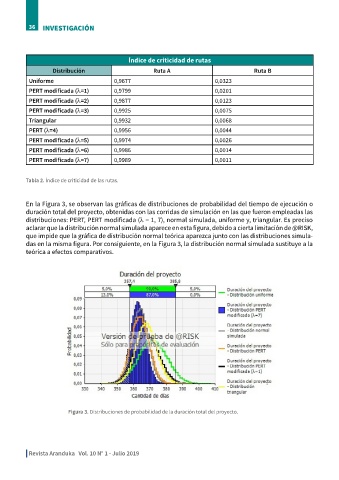
En la Figura 3, se observan las gráficas de distribuciones de probabilidad del tiempo de ejecución o alrededor del 33,65% de la varianza de la segunda. duración de ambas rutas han empatado; es decir,
duración total del proyecto, obtenidas con las corridas de simulación en las que fueron empleadas las Por consiguiente, la distribución de probabilidad en ninguna iteración de cada simulación dos rutas
distribuciones: PERT, PERT modificada (λ = 1, 7), normal simulada, uniforme y, triangular. Es preciso hallada a partir de la aplicación de la distribución resultaron ser críticas simultáneamente. Por consi-
aclarar que la distribución normal simulada aparece en esta figura, debido a cierta limitación de @RISK, uniforme, tiene una varianza cuyo valor corresponde guiente, el índice de criticidad de la ruta A equivale
que impide que la gráfica de distribución normal teórica aparezca junto con las distribuciones simula- a cerca de tres veces el valor de la varianza de la a restar a la unidad, el valor de dicho índice de la
das en la misma figura. Por consiguiente, en la Figura 3, la distribución normal simulada sustituye a la distribución normal dada por PERT. ruta B; es decir, los índices de criticidad de las men-
teórica a efectos comparativos. cionadas rutas se complementan. Otro resultado
La distribución de probabilidad más optimista de la a tener en cuenta, es que en todas las corridas de
duración del proyecto de entre todas las obtenidas, simulación realizadas, el índice de criticidad de la
corresponde a aquella en la que fue aplicada la ruta A ha sido superior a 0,96.
distribución PERT modificada con λ = 7; en la Figura
3 se observa que la gráfica de la misma posee una En las corridas en las que fue empleada la distri-
forma más empinada o puntiaguda que las demás, bución PERT modificada, el índice de criticidad
lo cual significa que hay una gran probabilidad de de la ruta A ha aumentado a medida que fue au-
ocurrencia asociada a los valores de tiempo (en días mentando el valor del parámetro λ; mientras que
corridos) que se encuentran alrededor de la media. lo contrario ocurre con el índice de criticidad de la
Por ende, los valores muy superiores a la media ruta B, lo cual es lógico, dado que ambos índices
tienen una probabilidad mayor de ocurrencia que son complementarios. Además, en la Figura 3 se
en las demás distribuciones generadas; es decir, la nota a medida que ha aumentado el valor de λ, la
probabilidad de culminar el proyecto en un tiem- forma de la gráfica de distribución se ha tornado
po mucho mayor a su media, es mayor que en las más empinada; siendo los valores considerados
demás distribuciones. Además, es la distribución para dicho parámetro iguales a 1, 4, 7.
obtenida con menor media y varianza.
El hecho de que la ruta A posea un índice de criti-
En la Figura 3 se observa que la gráfica de la distri- cidad tan alto en todas las corridas, indica que la
bución de probabilidad obtenida aplicando la distri- misma es dominante [16], es decir, dicha ruta posee
Figura 3. Distribuciones de probabilidad de la duración total del proyecto. bución uniforme, es la más achatada de todas. Por una duración mucho mayor a la de las demás. Por
otro lado, al igual que su varianza, la media de esta consiguiente, podría decirse que la necesidad de
distribución es la mayor de todas las distribuciones aplicar el método de Montecarlo para hallar índices
obtenidas. Por consiguiente, la probabilidad de cul- de criticidad es cuestionable en proyectos como el

Revista Aranduka Vol. 10 N° 1 - Julio 2019 Universidad Nacional de Asunción - Facultad Politécnica